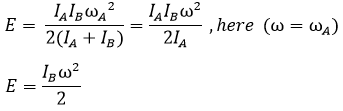Equation of Energy Loss by Friction Clutch During Engagement

Read: What is a Clutch? - Types of Clutches

Consider a plate or disc clutch
Let
I_A = mass moment inertia of rotors attached to shaft A
I_B = mass moment inertia of rotors attached to shaft B
ω_A = Angular speed of shat A before engagement
ω_B = Angular speed of shat B before engagement
ω = Common angular speed of shat A and Shaft B after engagement

According to the principle of conservation of momentum, Total momentum before clutch engage is equal to the total momentum of the clutch after clutch disc engagement.

IA ω_A + IB ω_B = (I_A + I_B)ω

Common angular speed after engagement of clutch pressure plate

ω= (I_A ω_A+I_B ω_B)/(I_A+I_B ) common angular speed

Total Kinetic energy before friction clutch engagement

E_1=1/2 I_A 〖ω_A〗^2+ 1/2 I_B 〖ω_B〗^2 E_1=1/2 〖(I〗_A 〖ω_A〗^2+I_B 〖ω_B〗^2) Energy equation before engagement

Kinetic energy after clutch engagement

E_2=1/2 〖(I〗_A+I_b)ω^2 energy equation after engagement

Put the value of ω into above equation,

E_2=1/2 〖(I〗_A+I_b)〖((I_A ω_A+I_B ω_B)/(I_A+I_B ))〗^2 = 〖〖(I〗_A ω_A+I_B ω_B)〗^2/(2(I_A+I_B)) energy equation after engagement of clutch

Now the loss of energy during clutch engagement, E= E₁-E₂

E= 1/2 〖(I〗_A 〖ω_A〗^2+I_B 〖ω_B〗^2)-〖〖(I〗_A ω_A+I_B ω_B)〗^2/(2(I_A+I_B)) E= (I_A I_B 〖(ω_A-ω_B)〗^2)/(2(I_A+I_B)) energy loss by friction during clutch engagement

🔗 Difference between Single Plate Clutch and Multi Plate Clutch

Apply Different condition for above equation
Condition I - The rotor attached and hence the shaft B at rest ω_B = 0
Put these condition in equation (a), and equation (b) we get
Common angular speed after the clutch engagement,

ω= (I_A ω_A)/(I_A+I_B ) coomon angular speed

Loss of kinetic energy

E= (I_A I_B 〖ω_A〗^2)/(2(I_A+I_B)) energy loss

Condition II - If rotor B at rest (ω_B = 0) and I_B is very small when compared to I_A
Common angular speed after the clutch engagement,

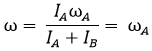
ω= (I_A ω_A)/(I_A+I_B )= ω_A common angular speed

Kinetic energy loss,